완전 이진 트리
[문제 링크] (https://www.acmicpc.net/problem/9934)
문제가 그렇게 어렵지는 않다.
그저 규칙 찾으면 끝나는 문제였다.
완전 이진 트리의 특성을 기억해보자.
완전 이진트리는 leaf 노드를 제외한 각 노드들은
자식을 2개씩 가지고 있다.
그리고 상근이는 도시에 있는 빌딩을 중순위(inorder traversal)방식으로 들어간다.
그리고 이미 들어갔던 곳은 안들어간다.
또, 고맙게도 완전 이진 트리이면서 포화 이진 트리이다(노드의 개수가 2^k -1개)
이제 문제다.
입력이 중순위 한 결과로 알려준다.
우리는 이 중순위 한 결과를 토대로 원래의 완전 이진 트리를 찾아야 한다(트리의 레벨에 따라 출력)
생각해보자.
항상 노드들은 개수가 2^level - 1개씩 있을 것이며, 각 레벨마다 노드의 개수가 2배씩 늘어난다.
1레벨에서는 1개, 2레벨에서는 2개, 3레벨에서는 4개, …
중순위 순회를 다시 한번 생각해보자.
왼쪽 노드, 중간 노드, 오른쪽 노드 순이다.
그러면! 포화 이진 트리이기 때문에 리프 노드들은 인덱스가 2개씩 차이 날 것이다.
이해가 잘 안될 수도 있다.
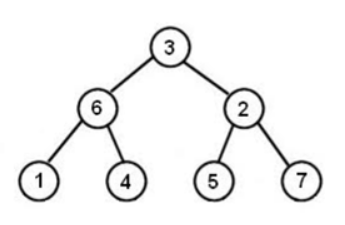
중순위 순회 특성상 가장 왼쪽노드 1을 먼저 방문할 것이다.
그 다음 중간 노드 6
그 다음 오른쪽 노드 4
그 다음은 3을 기준으로 왼쪽 트리 순회가 끝났기 때문에, 3이 중간노드로 3을 방문한다.
그러면 또 3을 기준으로 오른쪽 트리를 방문하지만 중순휘 순회 특성으로 오른쪽 트리의 맨 왼쪽 노드를 방문할 것이다.
이렇게 되면 1 -> 6 -> 4 -> 3 -> 5 -> 2 -> 7 순으로 방문하게 된다.
이제는 리프 노드들이 인덱스가 2개씩 차이나는 것이 보일 것이다.
그러면 그 리프 노드의 부모 노드는?
자식 노드들 + 1(부모 노드) + 1(자기 자신 차례) 개 차이 난다.
왜?
중순위 특성상 왼쪽 서브트리를 다 보고 자신을 보고 오른쪽 서브트리를 보기 때문에
어느 한 정점이 방문이 되었다면, 자신의 같은 레벨에 있는 노드까지의 거리는
자신의 오른쪽 서브트리의 노드의 개수 + 같은 레벨에 있는 노드의 왼쪽 서브트리의 노드의 개수 + 자신의 부모 노드이다.
오른쪽 서브트리 노드의 개수 + 왼쪽 서브트리의 노드의 개수 = 자식 노드의 개수
어디까지나 포화 이진트리에 한해서
이것은 리프 노드에 대입해도 같다.
따라서 자식의 개수는 2배씩 늘어나기 때문에 index jump를 2배씩 늘려주면 되는 문제다.
Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
int level;
vector<vector<int>>v;
vector<int>num;
bool visited[1025];
int main() {
ios_base::sync_with_stdio;
cin.tie(NULL); cout.tie(NULL);
int n;
cin >> n;
level = n;
num.reserve(level + 1);
int siz = 1;
for (int i = 0; i < n; i++) {
siz *= 2;
}
v.resize(siz);
for (int i = 1; i < siz; i++) {
int x;
cin >> x;
num.push_back(x);
}
int jump = 2;
for (int i = 0; i < siz / 2; i++) {
if (visited[i] == true) continue;
for (int j = i; j < siz - 1; j += jump) {
visited[j] = true;
v[level].push_back(num[j]);
}
level--;
jump *= 2;
}
for (int i = 1; i <= n; i++) {
for (int j = 0; j < v[i].size(); j++) {
cout << v[i][j] << " ";
}
cout << "\n";
}
}