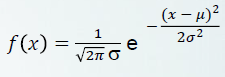Statistical Modeling
Bayes’ Rule
Nominal
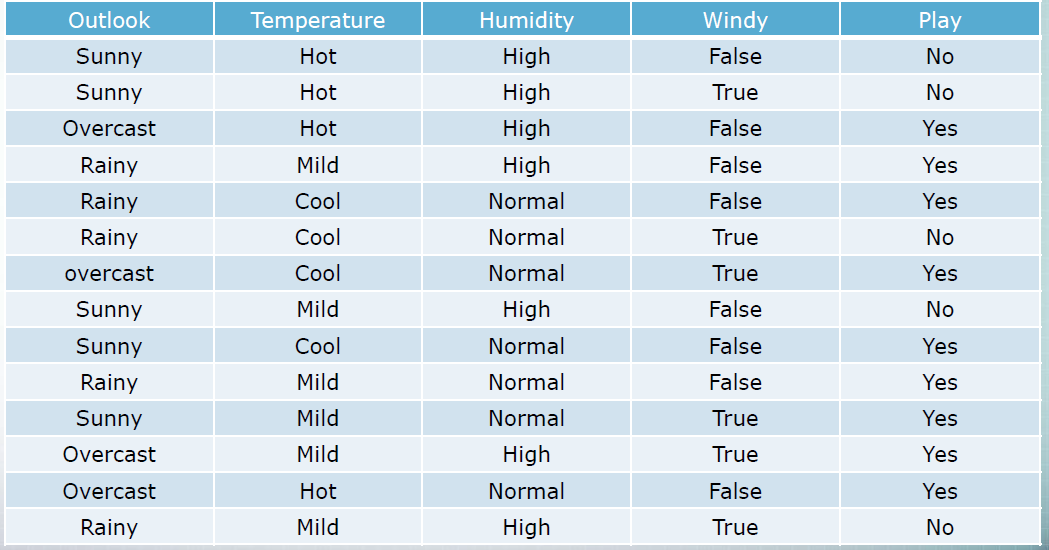
weatherdomain을 살펴보자.
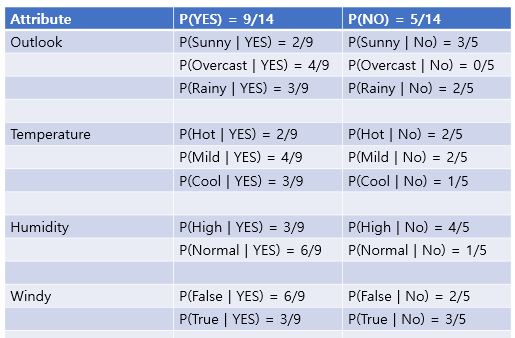
각각의 attribute의 probablity 값을 class의 yes no 기준으로 나눠 보자!!
이렇게 나뉜다.
New Instance
ex) Outlook = Rainy , Temperature = Mild , Humidity = Normal , Windy = False
이렇게 new Instance가 들어온다면 class의 값을 구해보자!
Likelihood of YES = 9/14(YES) * 3/9(Rainy and YES) * 4/9(Mild and YES) * 6/9(Normal and YES) * 6/9(False and YES)
= 0.04
Likelihood of NO = 5/14(NO) * 2/5(Rainy and NO) * 2/5(Mild and NO) * 1/5(Normal and NO) * 2/5(False and NO)
= 0.004
이제 이 식에 대입해보자.
| P(YES | E) = 0.04 / (0.04 + 0.004) = 0.91 |
| P(NO | E) = 0.004 / (0.04 + 0.004) = 0.09 |
여기서 Sigma j=1부터 n까지라는 뜻은 class의 모든 값의 합이다.
여기서는 Play = YES or NO
따라서 분모는 Likelihood of YES(0.04) + Likelihood of NO(0.004) 가 된다.
-> Nominal 값이 더 있다면 더 추가가 됐겠죠!?
| class의 모든 값의 합이기 때문에 P(YES | E) + P(NO | E) = 1 이 된다. (모든 경우의 수니까) |
따라서 new Instance의 대한 recommendation 은 YES(91.0%)가 나오게 된다.
Numeric
이산값이 어려웠다…
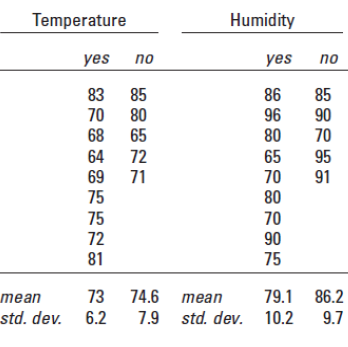
weatherdomain의 numeric 값을 보자.
이렇게 있는데
numeric 값의 평균과 표준 편차를 구해야 한다.
mean = 평균
std.dev = 표준 편차
표준 편차의 ^2 = 분산
이렇게 구하고
이 식에 집어 넣어야 한다!!
Likelihood of YES
시그마 값 = 표준 편차(6.2)
e = 자연로그의 밑
파이 = 3.14xxxx
x = new Instance의 numeric한 값
뮤 = 평균(73)
다 대입해서 Nomianl 처럼 값을 다 구해주면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
New Instance
outlook = sunny, temperature = 72, humidity = 80, windy = true then play = ?
구해보자!!
Likelihood of yes
-> 9/14 * 2/9 * 1.02293 * 1.0087 * 3/9 = 0.0491347
Likelihood of no
-> 5/14 * 3/5 * 1.11354 * 1.56451 * 3/5 = 0.22399
P(YES | E) = 0.0491347 / (0.0491347 + 0.22399) = 0.18
P(NO | E) = 0.22399 / (0.0491347 + 0.22399) = 0.82
따라서 New Instance 의 recommendation = "No" (82%) !!!
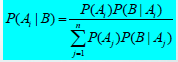
.PNG)