Decision tree
-
기계학습 알고리즘에 잘 맞는 방식 (다른 rule 보다)
-
효과적인 알고리즘
-
불확실성을 처리하기 위한 방법론
-
divide and conquer
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
예를 들어 보자
attribute outlook에 대해서 nominal data의 대한 값들이
sunny = {yes,yes,no,no,no}
overcast = {yes,yes,yes,yes}
rainy = {yes,yes,yes,no,no}
이렇게 있다고 가정 하자.
outlook overcast = yes 로 더 이상 나눌것이 없다.
-> Done! (conquered!)
-
decision tree의 root는 정보 분류 능력이 가장 좋은 것으로 선정!
-
entropy가 낮으면 정보 분류 능력이 높다!
-
entropy가 높으면 정보 분류 능력이 낮다!
Information
-
informaion = 정보의 bit 함유량
-
[0…1] 의 구간 값을 가진다
-
0은 더 이상 분류가 필요 없는 것 (전체가 conquer!!)
-
1은 정보 분류 능력이 하나도 없는 것
구하는 식
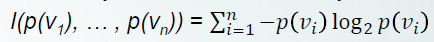
이다!!
weather domain 에서 play(class)의 값은 yes or no 밖에 없기 때문에 n = 2
yes = 9/14
no = 5/14
따라서 I(p/(p+n), n/(p+n)) = I(9/14, 5/14)
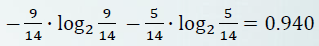
의 값이 된다.
Remainder
- 나눈 후에 더 나눠야 하는 것들에 대한 bit 요구량
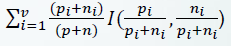
이 식에 대입한다!!
1
2
sunny yes,no overcast yes no rainy yes no
5/14 * I(2/5,3/5) + 4/14 * I(4/4,0/4) + 5/14 * I(3/5,2/5)
Gain
-
original informaion 요구량과 새로운 요구량의 차이!
-
음수가 될 수 없다
-
1을 넘을 수 없다
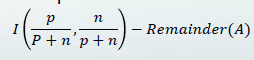
이중에서 가장 gain이 큰 attribute를 고른다!!!
왜? 정보 분류 능력이 가장 큰 것이기 때문이다
Gain이 크다는 뜻은 Remainder가 작다는 뜻이다.
따라서 Gain이 가장 클 때의 attribute를 고르면 정보 분류 능력이 가장 큰 것이다.